Definición de Convexo » Qué es, Significado y Concepto

Convexo es un término matemático usado para describir una figura, objeto o superficie en la que todos los puntos están dispuestos de manera tal que, si dos puntos se conectan con una línea, entonces esa línea permanecerá completamente dentro de la figura. Esto significa que, en un objeto convexo, cualquier línea que se encuentre entre dos puntos de la figura debe permanecer dentro de los límites del objeto.

Un objeto convexo es a menudo referido como una figura cerrada que no posee ángulos salientes o bordes afilados. Algunos ejemplos de objetos convexos incluyen un círculo, un triángulo equilátero, un cuadrado y un rectángulo. Estos objetos poseen superficies lisas y curvas, sin ningún borde afilado.

Los objetos convexos son útiles para realizar cálculos matemáticos. Muchos algoritmos de computación usan objetos convexos para realizar tareas como el reconocimiento de patrones, la compresión de imágenes y la detección de bordes en imágenes. También se usan para ilustrar problemas de optimización en los que uno necesita encontrar la mejor solución dentro de un conjunto de posibilidades.

Los objetos convexos también se usan en el campo de la geometría para describir la forma de una figura. Por ejemplo, un polígono es un objeto convexo si todos sus lados interiores están dispuestos de forma tal que no hay ángulos salientes. Esto significa que dos líneas que unen dos puntos de la figura deben estar dentro de sus límites.

¿Qué es un convexo?

¿Qué es un convexo? Un convexo es un polígono, un área o una frontera cerrada que no contiene ningún punto interior simplemente cerrado. Cualquier línea trazada entre dos puntos del borde del convexo estará completamente contenida en el interior.

Los convexos son muy útiles para la optimización matemática, ya que los problemas de optimización geométrica con límites convexos son mucho más fáciles de resolver. Esto se debe a que estos problemas tienen un único punto de optimización, por lo que los algoritmos de optimización pueden encontrar la solución óptima de forma rápida y precisa.

Los convexos también se usan en la geometría computacional para encontrar áreas y fronteras óptimas. Esto se debe a que los algoritmos de geometría computacional pueden hallar el área o la frontera interior más grande para un conjunto de puntos dado. Esto significa que los convexos se pueden usar para encontrar la forma óptima para un conjunto de puntos.

Los convexos también se usan en el procesamiento de imágenes, ya que las imágenes pueden ser representadas como un conjunto de convexos. Esto permite a los algoritmos de procesamiento de imágenes hallar el área o la frontera óptima para una imagen dada.

En resumen, un convexo es un polígono, área o frontera cerrada que no contiene ningún punto interior simplemente cerrado. Se usan en la optimización matemática, la geometría computacional y en el procesamiento de imágenes como una forma de encontrar áreas y fronteras óptimas.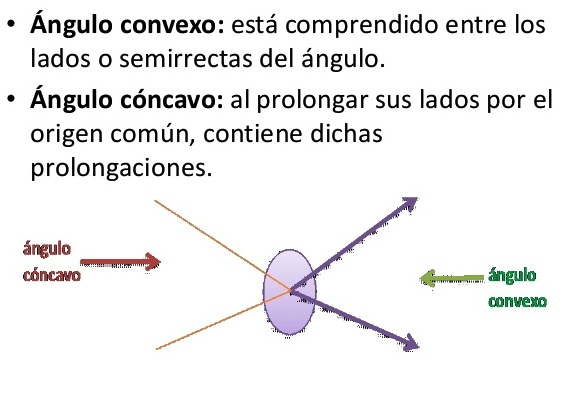

¿Qué es el cóncavo y convexo?

Cóncavo y convexo son dos conceptos relacionados con la forma de un objeto. El cóncavo se refiere a una superficie cuyo interior está hundido, como en una taza o un plato. Por el contrario, el convexo es una superficie cuyo exterior está hundido, como en una pelota. Estas dos formas tienen aplicaciones en muchas áreas, desde la medicina hasta la geometría.

En geometría, los cuerpos cóncavos se caracterizan por ser huecos y tener un interior hueco. Esto significa que el lado de afuera de un cuerpo cóncavo está curvado hacia adentro. Las figuras cóncavas también tienen superficies convexas, lo que significa que el lado de afuera está curvado hacia afuera. Por ejemplo, una concha es un cuerpo cóncavo con una superficie convexa.

Los cuerpos convexos se caracterizan por ser sólidos y tener un exterior hundido. Esto significa que el lado de afuera de un cuerpo convexo está curvado hacia adentro. Las figuras convexas también tienen superficies cóncavas, lo que significa que el lado de afuera está curvado hacia afuera. Por ejemplo, una pelota de fútbol es un cuerpo convexo con una superficie cóncava.

En medicina, los cóncavos y convexos se utilizan para describir la curvatura de la espalda. Una espalda cóncava se caracteriza por tener una curva hacia adentro en la parte media de la espalda. Una espalda convexa, por otro lado, se caracteriza por tener una curva hacia afuera en la parte media de la espalda. Estas formas se utilizan para medir la salud de la espalda y para ayudar a diagnosticar enfermedades como la escoliosis.

En resumen, cóncavo y convexo son dos conceptos relacionados con la forma de un objeto que tienen aplicaciones en muchas áreas, desde la medicina hasta la geometría. Un cuerpo cóncavo se caracteriza por tener un interior hueco y una superficie convexa, mientras que un cuerpo convexo tiene un exterior hundido y una superficie cóncava. Estas formas se utilizan en medicina para medir la salud de la espalda.

¿Qué es convexo y no convexo?

Convexo y no convexo son conceptos matemáticos que se aplican en la optimización de problemas. Una función es convexa si para cada punto en su dominio, hay una línea que une a los puntos y que permanece por encima de los puntos en la gráfica. Por el contrario, una función no convexa, tiene puntos que están por debajo de la línea que conecta los puntos.

Las funciones convexas son mucho más simples de analizar que sus contrapartes no convexas. Esto se debe a que para la optimización de funciones convexas se pueden usar técnicas matemáticas más simples y eficientes. Además, hay herramientas y métodos específicos que se pueden usar para optimizar funciones convexas.

• Las funciones convexas son aquellas que para cada punto en su dominio hay una línea que une a los puntos, que permanece por encima de los puntos en la gráfica.
• Las funciones no convexas tienen puntos que están por debajo de la línea que conecta los puntos.
• Las funciones convexas son más simples de analizar que sus contrapartes no convexas.
• Las herramientas y métodos específicos que se usan para optimizar funciones convexas son más simples y eficientes.

En la optimización de problemas, se usan técnicas de optimización diferentes dependiendo si la función es convexa o no convexa. Esto significa que el rendimiento del algoritmo depende de la naturaleza de la función. Por lo tanto, es importante tener en cuenta si una función es convexa o no convexa antes de intentar optimizarla.

¿Qué es una curvatura convexa?

Una curvatura convexa es una forma curva en un plano o en un espacio tridimensional que se extiende hacia afuera. Esto significa que, desde cualquier punto de esta curvatura, la dirección de la curvatura siempre se alejará de ese punto. Esta es una característica distintiva de las curvas convexas, y se encuentra en varias formas geométricas, desde medias lunas hasta líneas curvas. Esta característica se utiliza a menudo para definir la forma de los objetos en la geometría y la ingeniería.

Las curvas convexas se encuentran en la naturaleza en formas como olas, montañas y estructuras orgánicas. Esto se debe a que la convexidad se ajusta al principio de mínima energía, lo que significa que la curvatura convexa ayuda a los objetos a estabilizarse. Esto se debe a que la convexidad hace que los objetos sean menos susceptibles a la deformación externa o al cambio de forma, lo que evita que se deformen bajo fuerzas externas.

Además de la naturaleza, la curvatura convexa también se utiliza en la ingeniería para diseñar vehículos, construcciones y estructuras. Esto se debe a que la convexidad se ajusta al principio de máxima rigidez, lo que significa que la curvatura convexa es más resistente a la deformación externa. Esto hace que la curvatura convexa sea una forma adecuada para estructuras que deben soportar cargas externas.